" Joseph Louis Lagrange "

Giuseppe Lodovico Lagrangia (Lagrange), así fue bautizado, nació el 25 de enero de 1736 en Turín, donde creció y en cuya universidad cursó sus estudios de Leyes, en parte encaminado por su padre, aunque nunca obligado. De hecho, prefería el Latín clásico a la geometría griega, que la encontraba más bien aburrida. Sin embargo, a los 19 años esta visión cambió gracias a la lectura de una obra del astrónomo Edmund Halley sobre el uso del álgebra en la óptica. Este echo hizo que el joven Lagrange se interesara por las Matemáticas y tras un año de estudios era ya una brillante realidad matemática.
A los 19 años, escribió una carta a un tal Leonhard Euler en la que, utilizando por primera vez el cálculo de variaciones, resolvía un problema relacionado con la curva tautócrona (la cicloide, o auqella curva que hace que cualquier móvil, en ausencia de rozamiento, llegue de un punto a otro en el menor tiempo posible). Realmente, Euler ya estaba avanzando en el mismo problema, pero ante la generalidad del método descubierto por Lagrange, le cedió todo el mérito. 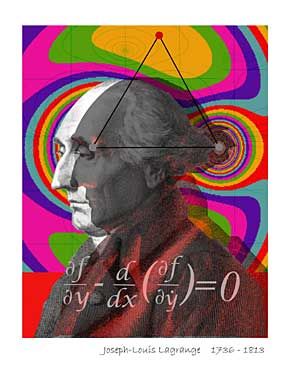En 1758, con la ayuda de sus alumnos, Lagrange publicó en la Academia de Turin la mayoría de sus primeros escritos consistentes en los cinco volúmenes, normalmente conocidos como Miscellanea Taurinensia y en 1761 ya era uno de los Matemáticos más reconocidos del panorama. Tal fue la admiración que Euler le profesaba, que lo propuso personalmente para su ingreso en la Academia de Berlín. En 1766 abandonó Berlín para incorporase a la corte prusiana de Federico el Grande, a petición particular del monarca, donde vivió sus años más prolíficos. Tras 20 años de estancia en San petersburgo y tras la muerte de Federico, aceptó un puesto en la Academia de París, la École normale y finalmente en la École Polytechnique. Lagrange murió en París el 10 de abril de 1813.
La obra matemática de Lagrange es extensísma. De sus años en Turín data su Miscellanea Taurinensia donde obtuvo, entre otros resultados, una ecuación diferencial general del movimiento y su adaptación para el caso particular del movimiento rectilíneo y la solución a muchos problemas de dinámica mediante el cálculo de variaciones.
Su trabajo en Berlín cubrió muchos temas: astronomía, la estabilidad del sistema solar, mecánica, dinámica, mecánica de fluidos, probabilidad, y los fundamentos del cálculo. También trabajó en la teoría de números demostrando en 1770 que todo entero positivo es la suma de cuatro cuadrados, y en 1771 el teorema de Wilson (p es primo si y sólo si (p-1)!+1 es divisible entre p).
Pero quizás por lo que es más conocido es por sus contribuciones a la teoría de funciones analíticas. Durante su estancia en la École Polytechnique, pronunció numerosas conferencias sobre este tema que suponen la base fundamental de sus obras Teoría de las funciones analíticas y Resolución de ecuaciones numéricas. Es en la primera de las obras donde aparece la demostración del Teorema del Valor Medio (hoy conocido como Teorema de Lagrange y que hace poco lo vimos colgado de un puente), mientras que en la segunda, proporciona un método para aproximar soluciones reales de ecuaciones gracias a las fracciones continuas.
Polinomios de Interpolación de Lagrange, Método de los Multiplicadores de Lagrange, Lagrangiano,... son sólo un pequeño ejemplo de la cantidad y calidad de las Matemáticas que hizo Joseph-Louis a lo largo de su vida.

Le gustaba la música. Decía que le aislaba y le ayudaba a pensar, ya que interrumpía la conversación general. “La escucho durante los tres primeros compases; luego no distingo nada, pero me entrego a mis pensamientos. De esta manera he resuelto muchos problemas difíciles”. Se casó dos veces: primero cuando vivía en Berlín, donde perdió a su esposa, después de una larga enfermedad, en la cual la cuidó con dedicación; luego en París, se casó nuevamente con la hija de un célebre astrónomo. Feliz en su vida hogareña, sencillo y bastante austero en sus gustos, pasó sus tranquilos años fructíferos, hasta que murió en 1813, a los setenta y seis años de edad.
      Esto es solo una pequeñisima parte de lo que se puede escribir de Lagrange.

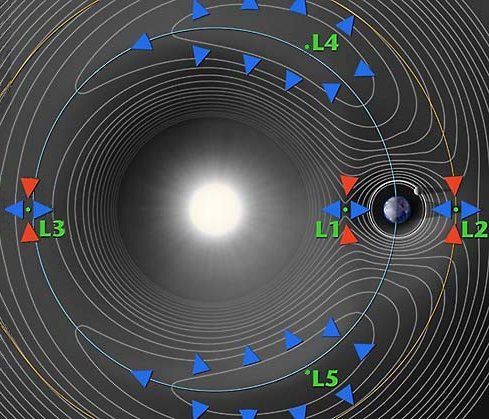Curvas de potencial en un sistema de dos-cuerpos (aquí el Sol y la Tierra), mostrando los cinco puntos de Lagrange. Las flechas indican pendientes alrededor de los puntos L – acercándose o alejándose de ellos. Contra la intuición, los puntos L4 y L5 son máximos.

Fuente: Eliatron.